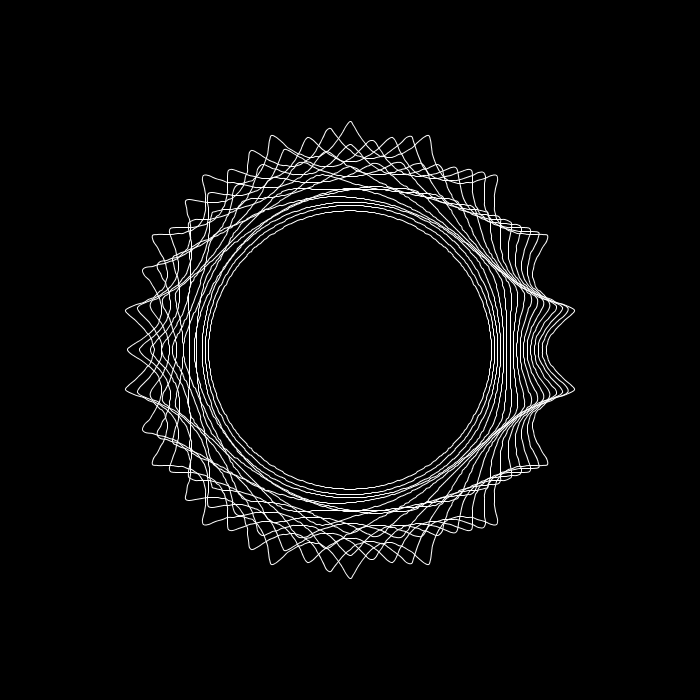
An old processing sketch in JRubyArt

# Visualize: Superformula
# from Form+Code in Design, Art, and Architecture
# by Casey Reas, Chandler McWilliams, and LUST
# Princeton Architectural Press, 2010
# ISBN 9781568989372
#
# Get Processing at http://www.processing.org/download

attr_reader :scaler, :m, :n1, :n2, :n3

def settings
  size(700, 700)
  smooth(4)
end

def setup
  sketch_title('Superformula')
  no_fill
  stroke(255)
  @scaler = 200.0
  @m = 2
  @n1 = 18.0
  @n2 = 1.0
  @n3 = 1.0
end

def draw
  background(0)
  push_matrix
  translate(width / 2, height / 2)
  newscaler = scaler
  16.downto(0) do |s|
    begin_shape
    mm = m + s
    nn1 = n1 + s
    nn2 = n2 + s
    nn3 = n3 + s
    newscaler *= 0.98
    sscaler = newscaler
    points = superformula(mm, nn1, nn2, nn3)
    curve_vertex(
      points[points.length - 1].x * sscaler,
      points[points.length - 1].y * sscaler
    )
    (0...points.length).each do |i|
      curve_vertex(points[i].x * sscaler, points[i].y * sscaler)
    end
    curve_vertex(points[0].x * sscaler, points[0].y * sscaler)
    end_shape
  end
  pop_matrix
end

def superformula(m, n1, n2, n3)
  num_points = 360
  phi = TWO_PI / num_points
  (0..num_points).map { |i| superformula_point(m, n1, n2, n3, phi * i) }
end

def superformula_point(m, n1, n2, n3, phi)
  t1 = cos(m * phi / 4)
  t1 = t1.abs
  t1 **= n2
  t2 = sin(m * phi / 4)
  t2 = t2.abs
  t2 **= n3
  r = (t1 + t2)**(1 / n1)
  return Vec2D.new if r.abs.zero?
  x = cos(phi) / r
  y = sin(phi) / r
  Vec2D.new(x, y)
end