VJaying with Visor
Jack V Purvis has created this excellent app Visor for live coding of Processing in the Ruby language. Visor attempts to empower Processing for live performance by combining elements from live coding and VJing practice. Turns out that JRubyArt is perfect for prototyping sketches for use in Visor, further there is a possibility for collaboration to create an even more awesome tool. Here is an example of Vec2D sketch in JRubyArt translated for Visor, that includes use of a custom gem to provide Vec2D and Vec3D classes.
# ===== Default : Default
GEM_HOME = '/home/tux/.gem/ruby/2.6.0'
require 'vecmath'
require 'forwardable'
# Here we use the JRubyArt Vec2D class, and not toxis Vec2D. We avoid using
# ToxicLibsSupport, by using our own AppRender to translate Vec2D to vertices.
# Further we use the power of ruby (metaprogramming) to make Branch enumerable
# and use Forwardable to define which enumerable methods we want to use.
visor_class :Branch do
include Enumerable
extend Forwardable
def_delegators(:@children, :<<, :each, :length)
# variance angle for growth direction per time step
THETA = Math::PI / 6
# max segments per branch
MAX_LEN = 100
# max recursion limit
MAX_GEN = 3
# branch chance per time step
BRANCH_CHANCE = 0.05
# branch angle variance
BRANCH_THETA = Math::PI / 3
attr_reader :position, :dir, :path, :children, :xbound, :speed, :ybound, :app
def initialize(pos, dir, speed)
@position = pos
@dir = dir
@speed = speed
@path = []
@children = []
@xbound = Boundary.new(0, 400)
@ybound = Boundary.new(0, 400)
path << pos
end
def run
grow
display
end
private
# NB: use of both rotate! (changes original) rotate (returns a copy) of Vec2D
def grow
check_bounds(position + (dir * speed)) if path.length < MAX_LEN
@position += (dir * speed)
dir.rotate!(rand(-0.5..0.5) * THETA)
path << position
if (length < MAX_GEN) && (rand < BRANCH_CHANCE)
branch_dir = dir.rotate(rand(-0.5..0.5) * BRANCH_THETA)
self << Branch.new(position.copy, branch_dir, speed * 0.99)
end
each(&:grow)
end
def display
beginShape
stroke(255)
no_fill
path.each { |vec| vertex(vec.x, vec.y) }
endShape
each(&:display)
end
def check_bounds(pos)
dir.x *= -1 if xbound.exclude? pos.x
dir.y *= -1 if ybound.exclude? pos.y
end
end
# we are looking for excluded values
Boundary = Struct.new(:lower, :upper) do
def exclude?(val)
!(lower...upper).cover? val
end
end
@root = Branch.new(
Vec2D.new(0, height / 2),
Vec2D.new(1, 0),
10.0
)
def draw
background(0)
root.run
end
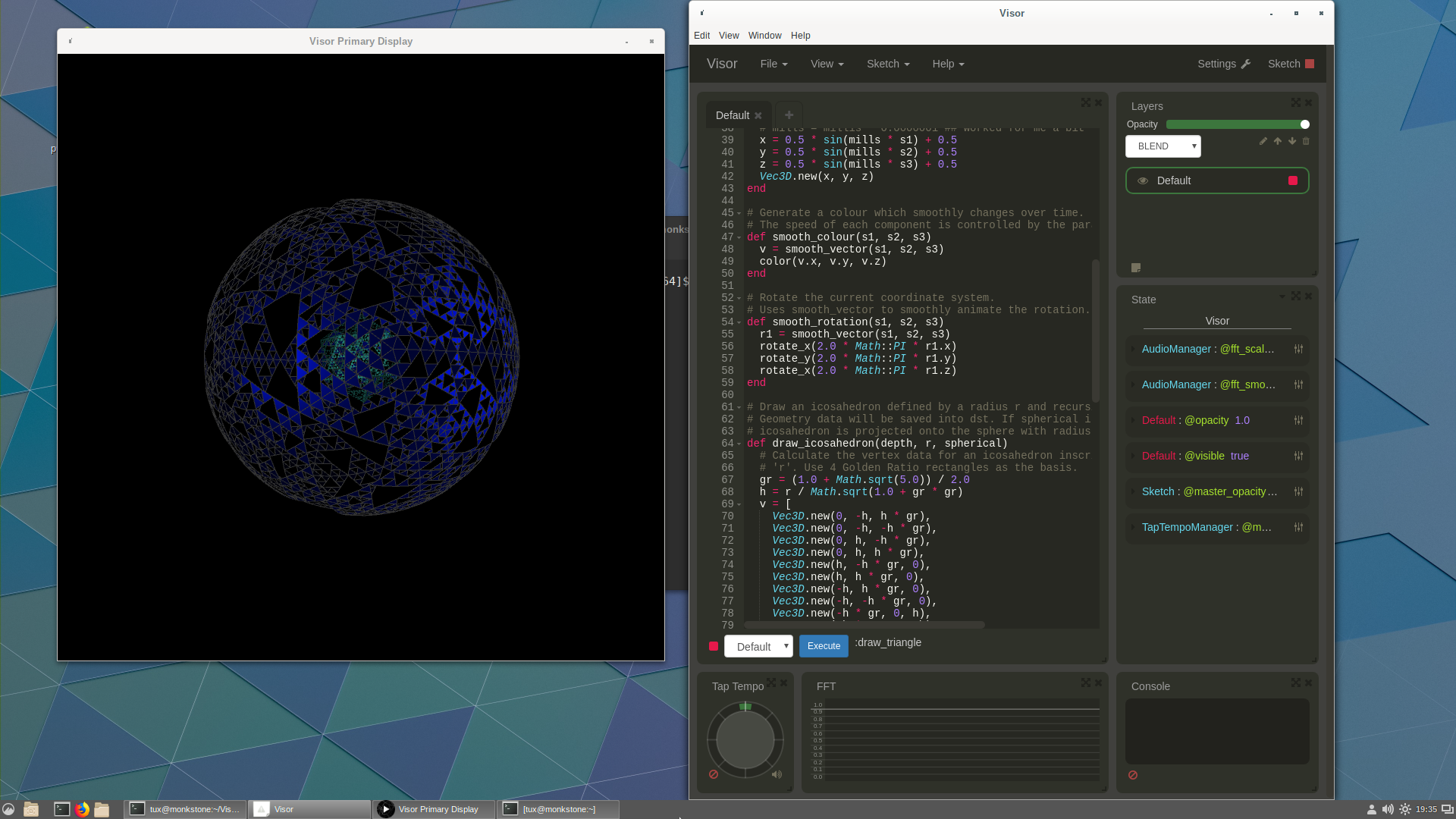
Here is a Vec3D sketch translated for Visor:-
# ===== Default : Default
GEM_HOME = '/home/tux/.gem/ruby/2.6.0'
require 'vecmath'
color_mode(RGB, 1)
def draw
background(0)
# Move the origin so that the scene is centered on the screen.
translate(width / 2, height / 2, 0.0)
# Set up the lighting.
setup_lights
# Rotate the local coordinate system.
smooth_rotation(5.0, 6.7, 7.3)
# Draw the inner object.
no_stroke
fill(smooth_colour(10.0, 12.0, 7.0))
draw_icosahedron(5, 60.0, false)
# Rotate the local coordinate system again.
smooth_rotation(4.5, 3.7, 7.3)
# Draw the outer object.
stroke(0.2)
fill(smooth_colour(6.0, 9.2, 0.7))
draw_icosahedron(5, 200.0, true)
end
def setup_lights
ambient_light(0.025, 0.025, 0.025)
directional_light(0.2, 0.2, 0.2, -1, -1, -1)
spot_light(1.0, 1.0, 1.0, -200, 0, 300, 1, 0, -1, PI / 4, 20)
end
# Generate a vector whose components change smoothly over time in the range
# (0..1). Each component uses a Math.sin function to map the current time in
# milliseconds in the range (0..1).A 'speed' factor is specified for each
# component.
def smooth_vector(s1, s2, s3)
mills = millis * 0.00003 ## Lazydogs factor
# mills = millis * 0.0000001 ## worked for me a bit slower!!
x = 0.5 * sin(mills * s1) + 0.5
y = 0.5 * sin(mills * s2) + 0.5
z = 0.5 * sin(mills * s3) + 0.5
Vec3D.new(x, y, z)
end
# Generate a colour which smoothly changes over time.
# The speed of each component is controlled by the parameters s1, s2 and s3.
def smooth_colour(s1, s2, s3)
v = smooth_vector(s1, s2, s3)
color(v.x, v.y, v.z)
end
# Rotate the current coordinate system.
# Uses smooth_vector to smoothly animate the rotation.
def smooth_rotation(s1, s2, s3)
r1 = smooth_vector(s1, s2, s3)
rotate_x(2.0 * Math::PI * r1.x)
rotate_y(2.0 * Math::PI * r1.y)
rotate_x(2.0 * Math::PI * r1.z)
end
# Draw an icosahedron defined by a radius r and recursive depth d.
# Geometry data will be saved into dst. If spherical is true then the
# icosahedron is projected onto the sphere with radius r.
def draw_icosahedron(depth, r, spherical)
# Calculate the vertex data for an icosahedron inscribed by a sphere radius
# 'r'. Use 4 Golden Ratio rectangles as the basis.
gr = (1.0 + Math.sqrt(5.0)) / 2.0
h = r / Math.sqrt(1.0 + gr * gr)
v = [
Vec3D.new(0, -h, h * gr),
Vec3D.new(0, -h, -h * gr),
Vec3D.new(0, h, -h * gr),
Vec3D.new(0, h, h * gr),
Vec3D.new(h, -h * gr, 0),
Vec3D.new(h, h * gr, 0),
Vec3D.new(-h, h * gr, 0),
Vec3D.new(-h, -h * gr, 0),
Vec3D.new(-h * gr, 0, h),
Vec3D.new(-h * gr, 0, -h),
Vec3D.new(h * gr, 0, -h),
Vec3D.new(h * gr, 0, h)
]
# Draw the 20 triangular faces of the icosahedron.
r = 0.0 unless spherical
begin_shape(TRIANGLES)
draw_triangle(depth, r, v[0], v[7], v[4])
draw_triangle(depth, r, v[0], v[4], v[11])
draw_triangle(depth, r, v[0], v[11], v[3])
draw_triangle(depth, r, v[0], v[3], v[8])
draw_triangle(depth, r, v[0], v[8], v[7])
draw_triangle(depth, r, v[1], v[4], v[7])
draw_triangle(depth, r, v[1], v[10], v[4])
draw_triangle(depth, r, v[10], v[11], v[4])
draw_triangle(depth, r, v[11], v[5], v[10])
draw_triangle(depth, r, v[5], v[3], v[11])
draw_triangle(depth, r, v[3], v[6], v[5])
draw_triangle(depth, r, v[6], v[8], v[3])
draw_triangle(depth, r, v[8], v[9], v[6])
draw_triangle(depth, r, v[9], v[7], v[8])
draw_triangle(depth, r, v[7], v[1], v[9])
draw_triangle(depth, r, v[2], v[1], v[9])
draw_triangle(depth, r, v[2], v[10], v[1])
draw_triangle(depth, r, v[2], v[5], v[10])
draw_triangle(depth, r, v[2], v[6], v[5])
draw_triangle(depth, r, v[2], v[9], v[6])
end_shape
end
##
# Draw a triangle either immediately or subdivide it first.
# If depth is 1 then draw the triangle otherwise subdivide first.
#
def draw_triangle(depth, r, p1, p2, p3)
if depth == 1
vertex p1.x, p1.y, p1.z
vertex p2.x, p2.y, p2.z
vertex p3.x, p3.y, p3.z
else
# Calculate the mid points of this triangle.
v1 = (p1 + p2) * 0.5
v2 = (p2 + p3) * 0.5
v3 = (p3 + p1) * 0.5
unless r == 0.0
# Project the vertices out onto the sphere with radius r.
v1.normalize!
v1 *= r
v2.normalize!
v2 *= r
v3.normalize!
v3 *= r
end
## Generate the next level of detail
depth -= 1
draw_triangle(depth, r, p1, v1, v3)
draw_triangle(depth, r, v1, p2, v2)
draw_triangle(depth, r, v2, p3, v3)
# Uncomment out the next line to include the central part of the triangle.
# draw_triangle(depth, r, v1, v2, v3)
end
end
Screenshot:-